9023. Minimum increments

An array of n positive integers is given. Find the minimum number of operations required to transform the array into an arithmetic progression with a difference of 1.

In one operation, you are allowed to increase any element of the array by 1.

Input. The first line contains a single integer n (n ≤ 10⁶).

The second line contains n positive integers, each not exceeding 10⁶.

Output. Print the minimum number of operations required to transform the array into an arithmetic progression with a difference of 1.

Explanation. In the first test, the array should be transformed into:

8 9 10 11 12

To do this, we need

(8 – 3) + (9 – 6) + (10 – 4) + (11 – 11) + (12 – 5) = 5 + 3 + 6 + 0 + 7 = 21

operations.

Sample input 1	Sample output 1
5 3 6 4 11 5	21
Sample input 2	Sample output 2
5 4 4 5 5 7	5

РЕШЕНИЕ

binary search

Algorithm analysis

Let the minimum number of operations transform the original array

m[0], m[1], …, m[n – 1]

into an arithmetic progression of the form

x, x + 1, x + 2, …, x + n – 1

Obviously, m[0] ≤ x ≤ max(m[0], m[1], …, m[n – 1]).

We call the sequence

d = [x, x + 1, x + 2, …, x + n – 1]

valid if array m can be transformed into d, i.e., if the condition m[i] ≤ d[i] holds for all i from 0 to n – 1.

It remains to find the smallest value of x for which the sequence d is valid. This can be done using binary search.

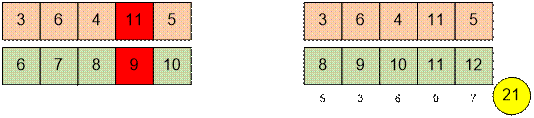
Example

Consider the first test case. Let d = [x, x + 1, x + 2, …, x + n – 1] be a valid sequence with the minimal possible sum of elements.

Obviously, m[0] = 3 ≤ x ≤ 11 = max(m[i]).

Using binary search, find the smallest value of x for which the sequence d is valid.

For example, when x = 6, the sequence d is not valid, but when x = 8, it is.

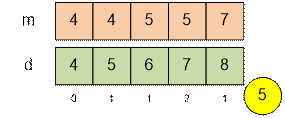
Now consider the second test case. Run binary search in the interval 4 ≤ x ≤ 7. For example, the sequence d is already valid at x = 4.

Algorithm implementation

The input sequence is stored in the array m. The sequence x, x + 1, x + 2, …, x + n – 1 is stored in the array d.

#define MAX 1000000

int m[MAX], d[MAX];

The function check generates in array d a sequence of the form:

first, first + 1, first + 2, …, first + n – 1

If for every i (0 ≤ i ≤ n – 1) the condition m[i] ≤ d[i] holds, then array d can be obtained from array m by incrementing some elements by 1. In this case, the array d is considered valid. If the array d is valid, the function check returns 1, otherwise it returns 0.

int check(int first)

{

for (int i = 0; i < n; i++)

d[i] = first++;

for (int i = 0; i < n; i++)

if (m[i] > d[i]) return 0;

return 1;

}

The main part of the program. Read the input value n. Compute the maximum value mx in the array m.

scanf("%d", &n);

mx = 0;

for (i = 0; i < n; i++)

{

scanf("%d", &m[i]);

if (m[i] > mx) mx = m[i];

}

start = m[0];

end = mx;

Start a binary search for the value x in the interval [start; end] = [m[0]; mx].

The goal is to find the smallest value of x such that the sequence x, x + 1, x + 2, …, x + n – 1 can be obtained from the array m[0], m[1], …, m[n – 1].

while (start < end)

{

mid = (start + end) / 2;

if (check(mid))

end = mid;

else

start = mid + 1;

}

Generate the desired arithmetic progression.

for (i = 0; i < n; i++)

d[i] = start++;

Compute the minimum number of operations required to obtain this progression.

op = 0;

for (int i = 0; i < n; i++)

op += (d[i] - m[i]);

Print the answer.

printf("%lld\n", op);